①在得到预测值时有疑问

在视频中老师给的数据是

X = np.array([[600, 0.8], [800, 1.2],
              [1500, 10], [2500, 3]])
y = np.array([14, 16, 24, 26])

预测得到的结果是18.374,18.916,21.084,21.626

是通过第3棵树的残差进行梯度提升得到-4.374, -2.916, 2.916, 4.374

用y的值减去对应残差而得

但我不理解若我给定测试数据X1，没有对应y1，是如何计算出预测值的

X1 = np.array([[1000, 1.5], [1800, 0.8],
              [1500, 0], [3500, 4]])

程序对于我的X1是18.916,20.284000000000002,20.284000000000002,21.626

②这一问题还是对于预测值有疑问

如图，我只对老师的代码进行了树深度修改，改为1，树为第三颗树的图，按照老师视频中讲述的

最后残差为 residual = residual_3 - residual_3 * learning_rate=[-3.645，-3.645，3.645，3.645]

那么用y值减去残差应该得到[17.645, 19.645, 20.355, 22.355]，但这就跟程序运行出来有差异

此时对于我自己给定的X1,程序输出的预测值我也不是很懂怎么出来的，希望老师对我这两个问题解释一下

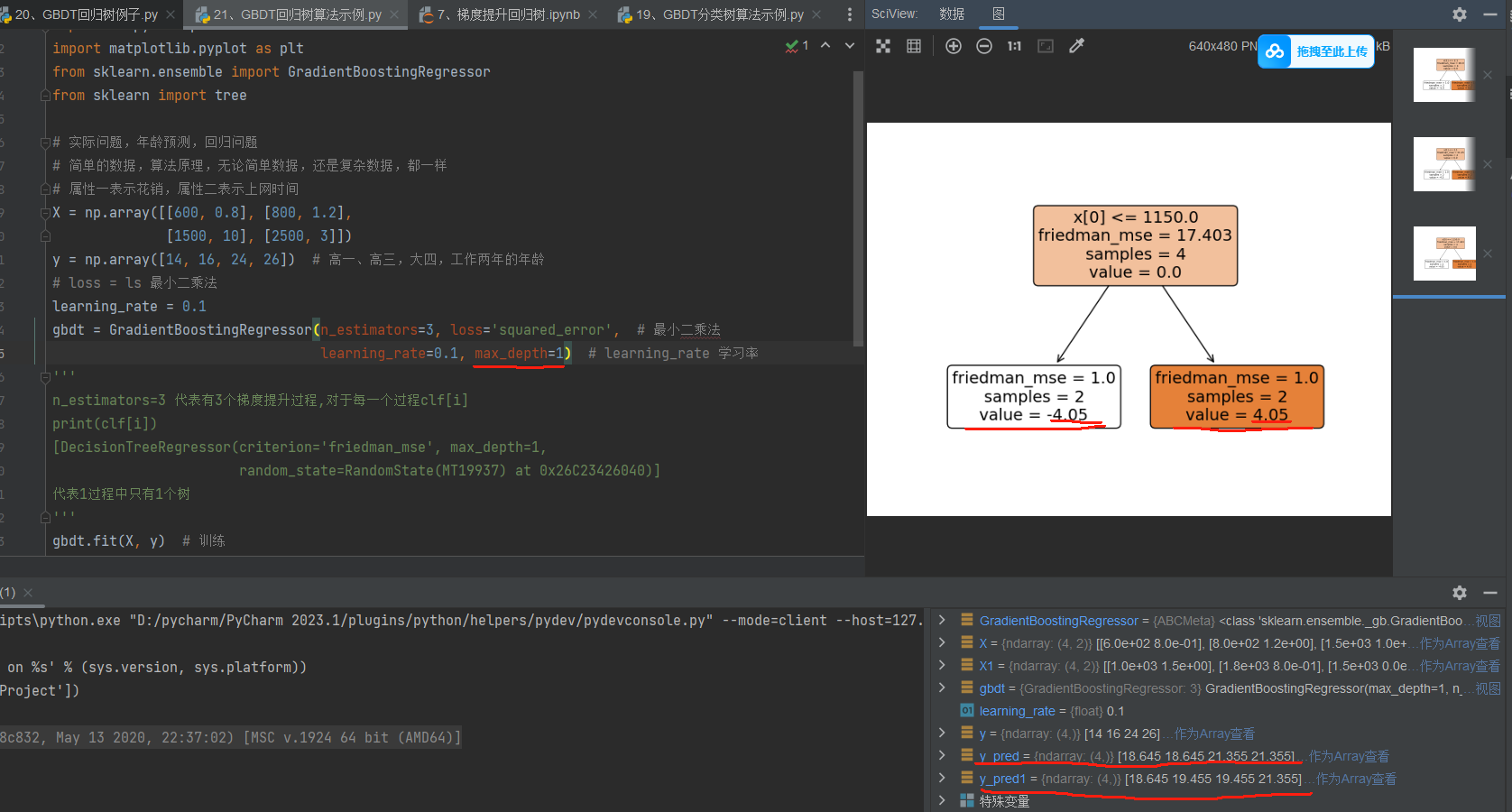
代码如下：

import numpy as np
import matplotlib.pyplot as plt
from sklearn.ensemble import GradientBoostingRegressor
from sklearn import tree

# 实际问题，年龄预测，回归问题
# 简单的数据，算法原理，无论简单数据，还是复杂数据，都一样
# 属性一表示花销，属性二表示上网时间
X = np.array([[600, 0.8], [800, 1.2],
              [1500, 10], [2500, 3]])
y = np.array([14, 16, 24, 26])  # 高一、高三，大四，工作两年的年龄
# loss = ls 最小二乘法
learning_rate = 0.1
gbdt = GradientBoostingRegressor(n_estimators=3, loss='squared_error',  # 最小二乘法
                                 learning_rate=0.1, max_depth=1)  # learning_rate 学习率
'''
n_estimators=3 代表有3个梯度提升过程,对于每一个过程clf[i]
print(clf[i])
[DecisionTreeRegressor(criterion='friedman_mse', max_depth=1,
                       random_state=RandomState(MT19937) at 0x26C23426040)]
代表1过程中只有1个树
'''
gbdt.fit(X, y)  # 训练
y_pred = gbdt.predict(X)  # 预测
X1 = np.array([[1000, 1.5], [1800, 0.8],
              [1500, 0], [3500, 4]])
y_pred1 = gbdt.predict(X1)
# 画第一颗树
tree.plot_tree(gbdt[0, 0], filled=True, rounded=True)
plt.show()
tree.plot_tree(gbdt[1, 0], filled=True, rounded=True)
plt.show()
tree.plot_tree(gbdt[2, 0], filled=True, rounded=True)
plt.show()